Геометрическое свойство выпуклых четырехугольников, согласно которому сумма их внутренних углов составляет 360 градусов, имеет строгое математическое обоснование. Рассмотрим доказательство этого фундаментального положения.
Содержание
Математическое доказательство
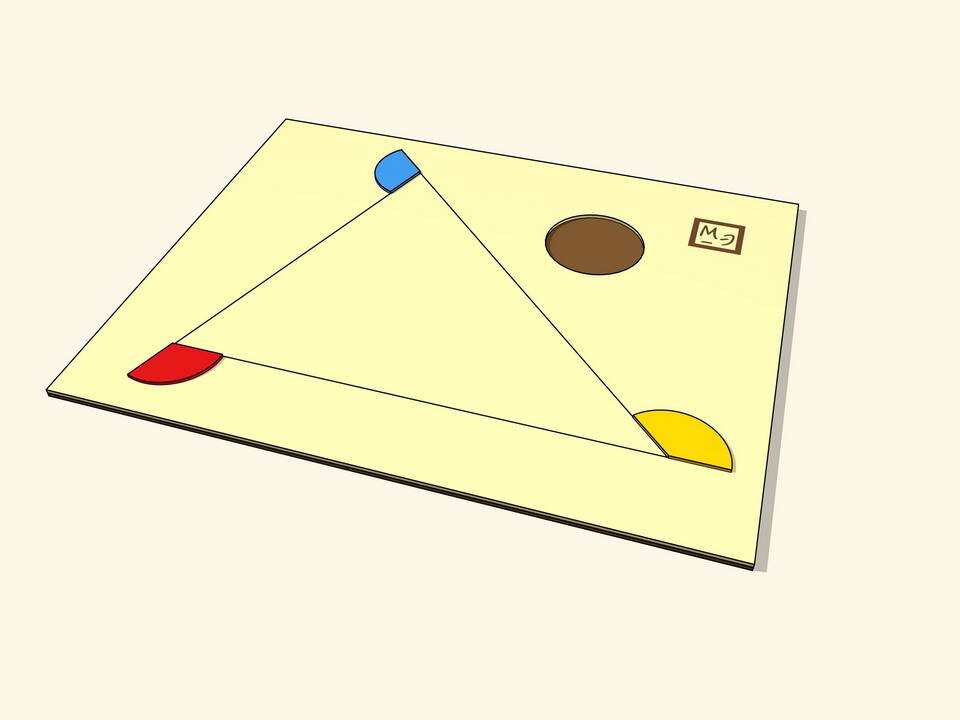
- Разбиение на треугольники - любой выпуклый четырехугольник можно разделить диагональю на два треугольника
- Свойство треугольников - сумма углов каждого треугольника равна 180°
- Суммирование - 180° × 2 = 360° для четырехугольника
- Обобщение - метод работает для любого выпуклого n-угольника: (n-2) × 180°
Сравнение многоугольников
| Фигура | Количество сторон | Сумма углов |
| Треугольник | 3 | 180° |
| Четырехугольник | 4 | 360° |
| Пятиугольник | 5 | 540° |
Доказательство через внешние углы
- Сумма внешних углов многоугольника всегда 360°
- Внутренний и внешний углы в каждой вершине дают в сумме 180°
- Для n вершин: n × 180° - 360° = сумма внутренних углов
- Для четырехугольника: 4 × 180° - 360° = 360°
Практическое значение свойства
- Проверка правильности построения фигур
- Расчет недостающих углов в задачах
- Доказательство других геометрических теорем
- Применение в архитектуре и инженерии
Равенство суммы углов выпуклого четырехугольника 360 градусам является следствием более общего правила для выпуклых многоугольников и подтверждается несколькими независимыми методами доказательства. Это фундаментальное свойство широко применяется в геометрических расчетах и построениях.