Сумма синуса и косинуса одного и того же угла представляет собой важное тригонометрическое выражение, которое можно преобразовать к более компактному виду. Рассмотрим свойства и методы вычисления этого выражения.
Содержание
Основная формула преобразования
Сумму синуса и косинуса можно выразить через одну тригонометрическую функцию:
sin α + cos α = √2 sin(α + π/4) = √2 cos(α - π/4)
Вывод формулы
- Используем формулу синуса суммы: sin(α + β) = sin α cos β + cos α sin β
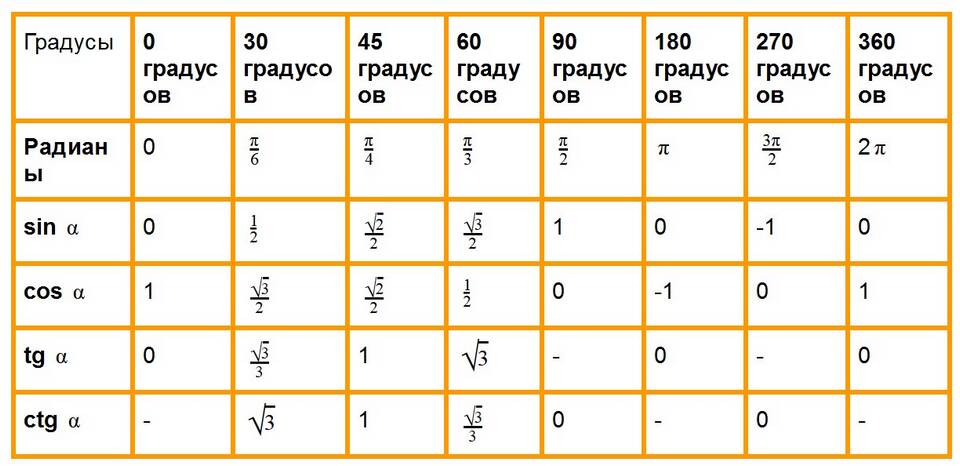
- Принимаем β = π/4 (45°), тогда cos β = sin β = √2/2
- Получаем: √2 sin(α + π/4) = √2(sin α · √2/2 + cos α · √2/2) = sin α + cos α
Свойства выражения sin α + cos α
| Свойство | Значение |
| Область значений | [-√2, √2] |
| Максимальное значение | √2 (при α = π/4 + 2πn) |
| Минимальное значение | -√2 (при α = 5π/4 + 2πn) |
| Нули функции | α = 3π/4 + πn, n∈ℤ |
Графическая интерпретация
График функции y = sin x + cos x представляет собой синусоиду с:
- Амплитудой √2 ≈ 1.414
- Периодом 2π
- Фазовым сдвигом π/4 влево
Практическое применение
Решение уравнений
Уравнения вида sin x + cos x = a решаются с помощью преобразования: √2 sin(x + π/4) = a
Вычисление интегралов
∫(sin x + cos x)dx = -cos x + sin x + C
Анализ колебаний
Сумма гармонических колебаний одинаковой частоты может быть представлена как одно колебание
Частные случаи
| Угол α | Значение sin α + cos α |
| 0 | 0 + 1 = 1 |
| π/4 (45°) | √2/2 + √2/2 = √2 ≈ 1.414 |
| π/2 (90°) | 1 + 0 = 1 |
| π (180°) | 0 + (-1) = -1 |
Дополнительные формулы
- (sin α + cos α)² = 1 + sin 2α
- sin α + cos α = √(1 + sin 2α)
- sin α + cos α = 2 sin(α/2 + π/8) cos(α/2 - π/8)
Методы запоминания
- Запомнить коэффициент √2 и сдвиг π/4
- Представить графическое сложение двух функций
- Ассоциировать с формулой сложения гармонических колебаний
Ошибки при работе с выражением
- Попытка представить сумму как синус или косинус без коэффициента √2
- Неправильное определение фазового сдвига
- Игнорирование области значений выражения